Tölvunarfræði 2 - Vor 2012
Verkefni 10
Lausnum skal skilað til viðkomandi dæmakennara (sjá lista yfir dæmatíma).
Reynið að skrifa stutt, skýr og hnitmiðuð forrit. Notið réttan inndrátt og gætið þess að forritin ykkar séu læsileg.
Skiladagur: þriðjudaginn 20. mars fyrir kl 16:00
Dæmi 1 (2 stig) - Innsetning í tvíleitartré
Leysið dæmi 3.2.1 í bókinni.
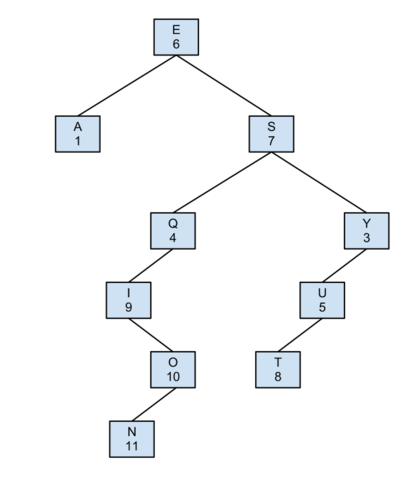
Draw the BST that results when you insert the keys E A S Y Q U E S T I O N, in that order (associating the value i with the ith key, as per the convention in the text) into an initially empty tree. How many compares are needed to build the tree?
Lausn
Dæmi 2 (2 stig) - Hæð fyrir tvíleitartré
Leysið dæmi 3.2.6 í bókinni.
Add to BST a method height() that computes the height of the tree. Develop two implementations: a recursive method (which takes linear time and space proportional to the height), and a method like size() that adds a field to each node in the tree (and takes linear space and constant time per query).
Beinagrind fyrir tvíleitartré: BST.java. Athugið að endurkvæm height() aðferð fylgir með beinagrindinni. Þið ættuð samt að reyna að skrifa ykkar eigin útgáfu frá grunni og skilja nákvæmlega hvernig hún virkar.
Endurkvæm lausn sem reiknar hæðina
public int height()
{
return height(root);
}
private int height(Node x)
{
if (x == null) return -1;
return 1 + Math.max(height(x.left), height(x.right));
}
Lausn sem geymir og viðheldur hæðinni í breytu í hverjum hnút
private class Node {
private Key key; // sorted by key
private Value val; // associated data
private Node left, right; // left and right subtrees
private int N; // number of nodes in subtree
private int height; // height of subtree
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
this.height = 0;
}
}
public int height()
{
return height(root);
}
private int height(Node x)
{
if (x == null) return 0;
return x.height;
}
public void put(Key key, Value val) {
if (val == null) { delete(key); return; }
root = put(root, key, val);
assert check();
}
private Node put(Node x, Key key, Value val) {
if (x == null) return new Node(key, val, 1);
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = put(x.left, key, val);
else if (cmp > 0) x.right = put(x.right, key, val);
else x.val = val;
x.N = 1 + size(x.left) + size(x.right);
x.height = 1 + Math.max(height(x.left), height(x.right));
return x;
}
public void deleteMin() {
if (isEmpty()) throw new RuntimeException("Symbol table underflow");
root = deleteMin(root);
assert check();
}
private Node deleteMin(Node x) {
if (x.left == null) return x.right;
x.left = deleteMin(x.left);
x.N = size(x.left) + size(x.right) + 1;
x.height = 1 + Math.max(height(x.left), height(x.right));
return x;
}
public void deleteMax() {
if (isEmpty()) throw new RuntimeException("Symbol table underflow");
root = deleteMax(root);
assert check();
}
private Node deleteMax(Node x) {
if (x.right == null) return x.left;
x.right = deleteMax(x.right);
x.N = size(x.left) + size(x.right) + 1;
x.height = 1 + Math.max(height(x.left), height(x.right));
return x;
}
public void delete(Key key) {
root = delete(root, key);
assert check();
}
private Node delete(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = delete(x.left, key);
else if (cmp > 0) x.right = delete(x.right, key);
else {
if (x.right == null) return x.left;
if (x.left == null) return x.right;
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.N = size(x.left) + size(x.right) + 1;
x.height = 1 + Math.max(height(x.left), height(x.right));
return x;
}
Dæmi 3 (2 stig) - Innsetning í hrúgu
Leysið dæmi 2.4.5 í bókinni.
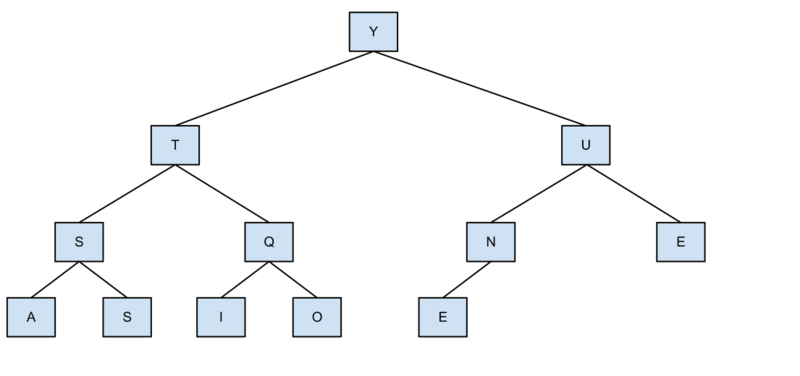
Give the heap that results when the keys E A S Y Q U E S T I O N are inserted in that order into an initially empty max-oriented heap.
Lausn
Dæmi 4 (4 stig) - Forgangsbiðröð byggð á hrúgu með hlekkjum (ekki hrúgu í fylki)
Leysið dæmi 2.4.24 í bókinni.
Priority queue with explicit links. Implement a priority queue using a heap-ordered binary tree, but use a triply linked structure instead of an array. You will need three links per node: two to traverse down the tree and one to traverse up the tree. Your implementation should guarantee logarithmic running time per operation, even if no maximum priority-queue size is known ahead of time.
Skrifið notkunarlýsingu fyrir öll föll sem þið skrifið. Skrifið fastayrðingu gagna fyrir útfærslu ykkar á forgangsbiðröðinni. Skrifið fastayrðingu lykkju fyrir allar lykkjur sem þið skrifið.
Það er líka hægt að útfæra þetta án þess að geyma tilvísun á foreldri í hverjum hnút og ef þið gerið það þannig þá megið þið sleppa parent tilviksbreytunni og halda bara utan um tilvísun á vinstra og hægra undirtré.
Vísbending: þið getið geymt fjölda gilda í hverjum hnút (eins og size í BST) og notað það í innsetningu til að setja gildi á réttan stað í trénu þ.a. það fylli hverja hæð áður en það byrjar á næstu hæð.
Lausn
public class PriQueue
{
// Gildin í forgangsbiðröðinni eru í hrúgu
// með stærsta stak efst, root vísar á rótina
// fyrir hrúguna.
// Allar hæðir eru fullskipaðar nema e.t.v. sú
// neðsta.
private Node root;
private static class Node
{
private String val;
private Node left, right;
private Node parent;
int height;
public Node(String val)
{
this.val = val;
this.height = 0;
}
}
// Notkun: pq = new PriQueue();
// Fyrir: Ekkert
// Eftir: pq er ný tóm forgangsbiðröð
public PriQueue()
{
root = null;
}
private static void fixUp(Node x)
{
while (x != null)
{
x.height = 1 + Math.max(height(x.left), height(x.right));
x = x.parent;
}
}
// Notkun: x = pq.findBottomLeaf(root);
// Fyrir: Ekkert
// Eftir: x er lauf á neðstu hæðinni í trénu root
private static Node findBottomLeaf(Node root)
{
Node x = root;
while (!isLeaf(x))
{
if (height(x.left) > height(x.right))
x = x.left;
else
x = x.right;
}
return x;
}
private static boolean isLeaf(Node x)
{
return x.left == null && x.right == null;
}
// Notkun: root = pq.removeLeaf(x);
// Fyrir: x er lauf
// Eftir: root er rót nýja hrúgu trésins sem kemur
// út þegar hnútnum x er eytt úr trénu
private static Node removeLeaf(Node x)
{
if (x.parent == null)
return null;
if (x.parent.left == x)
x.parent.left = null;
else
x.parent.right = null;
while (x.parent != null)
{
x.height = 1 + Math.max(height(x.left), height(x.right));
x = x.parent;
}
return x;
}
private static void rolldown(Node root)
{
Node x = root;
while (!isLeaf(x))
{
// root er hrúga nema e.t.v. er
// gildið í x of ofarlega
Node b = x.left;
if (x.left == null)
b = x.right;
else if (x.right != null && x.left.val.compareTo(x.right.val) < 0)
b = x.right;
if (x.val.compareTo(b.val) > 0)
break;
swap(x, b);
x = b;
}
}
// Notkun: s = pq.deleteMax();
// Fyrir: pq er ekki tóm.
// Eftir: s er eitt stærsta gildið sem var
// í pq. s hefur verið fjarlægt úr pq.
public String deleteMax()
{
String result = root.val;
Node last = findBottomLeaf(root);
root = removeLeaf(last);
if (root != null)
{
root.val = last.val;
rolldown(root);
}
return result;
}
private static void swap(Node a, Node b)
{
String tmp = a.val;
a.val = b.val;
b.val = tmp;
}
// Notkun: pq.put(s);
// Fyrir: pq er ekki full.
// Eftir: s hefur verið bætt við pq.
public void put(String s)
{
root = put(root, s);
}
private static Node put(Node x, String s)
{
if (x == null)
return new Node(s);
if (s.compareTo(x.val) > 0)
{
String tmp = x.val;
x.val = s;
s = tmp;
}
int ls = height(x.left);
int rs = height(x.right);
if (ls <= rs)
{
x.left = put(x.left, s);
x.left.parent = x;
}
else
{
x.right = put(x.right, s);
x.right.parent = x;
}
x.height = 1 + Math.max(height(x.left), height(x.right));
return x;
}
public static int height(Node x)
{
if (x == null) return -1;
return x.height;
}
public static void prettyPrint(int level, Node root)
{
if (level > 0)
{
for (int i = 0; i < level*2; i++)
System.out.print(" ");
}
if (root == null)
{
System.out.print("()\n");
return;
}
if (root.left != null || root.right != null)
{
System.out.printf("(%s[%d]\n", root.val, root.height);
prettyPrint(level+1, root.left);
prettyPrint(level+1, root.right);
for (int i = 0; i < level*2; i++)
System.out.print(" ");
System.out.println(")");
} else
{
System.out.printf("%s[%d]\n", root.val, root.height);
}
}
public void prettyPrint()
{
prettyPrint(0, root);
System.out.println();
}
public boolean isEmpty()
{
return root == null;
}
public static void main(String[] args)
{
PriQueue pq = new PriQueue();
pq.put("F");
pq.put("B");
pq.put("D");
pq.put("C");
pq.put("A");
pq.put("H");
pq.put("P");
pq.put("C");
pq.put("Q");
pq.put("T");
pq.prettyPrint();
System.out.println("------------");
while (!pq.isEmpty())
{
System.out.println(pq.deleteMax());
pq.prettyPrint();
}
}
}