Tölvunarfræði 2 - Vor 2012
Verkefni 8
Lausnum skal skilað til viðkomandi dæmakennara (sjá lista yfir dæmatíma).
Reynið að skrifa stutt, skýr og hnitmiðuð forrit. Notið réttan inndrátt og gætið þess að forritin ykkar séu læsileg.
Skiladagur: þriðjudaginn 6. mars fyrir kl 16:00
Dæmi 1 (2 stig) - Quickselect og miðgildi
Útfærið quickselect í beinagrindinni með hjálp partition fallsins úr quicksort. Útfærið síðan fallið median í beinagrindinni með hjálp quickselect. Median fallið á að finna miðgildi í óröðuðu fylki heiltalna á O(N) tíma.
Ef stærð fylkisins er jöfn tala þá er miðgildið meðaltal miðjustakanna tveggja. Þið getið skoðað nokkur dæmi á Wikipedia.
Beinagrind fyrir Java
import java.util.Random;
public class Quickselect
{
// Notkun: select(f,i,j,k)
// Fyrir: f[i..j-1] er svæði í fylkinu f, i <= k < j
// f[i..j-1] má vera óraðað.
// Eftir: Búið er að víxla gildunum í f[i..j-1] þannig
// að f[i..k-1] <= f[k] <= f[k+1..j-1].
public static void select(int[] f, int i, int j, int k)
{
// ...
}
// Notkun: m = median(f);
// Fyrir: Ekkert
// Eftir: m er miðgildi f
public static double median(int[] f)
{
// ...
}
// Notkun: k = partition(f,i,j,s);
// Fyrir: f[i..j-1] er löglegt svæði í f,
// i <= s < j
// f[s] er pivot gildi til að skipta eftir
// Eftir: Búið er að víxla gildum í svæðinu þ.a.
// f[i..k-1] <= f[k] <= f[k+1..j-1]
// Gildið í sæti k var upphaflega í sæti s.
public static int partition(int[] f, int i, int j, int s)
{
// Úr V7
}
// Notkun: b = is_partitioned(f,i,j,k)
// Fyrir: f[i..j-1] er svæði í fylkinu f, i <= k < j
// f[i..j-1] má vera óraðað.
// Eftir: b er satt þþaa. að
// f[i..k-1] <= f[k] <= f[k+1..j-1].
static boolean is_partitioned(int[] f, int i, int j, int k)
{
for (int n = i; n != k; n++)
if (f[n] > f[k])
return false;
for (int n = k; n != j; n++)
if (f[n] < f[k])
return false;
return true;
}
private static void swap(int[] f, int a, int b)
{
int tmp = f[a];
f[a] = f[b];
f[b] = tmp;
}
public static void main(String[] args)
{
Random g = new Random();
for (int n = 0; n < 5; n++)
{
int[] f = {62,88,59,94,4,71,26,17,44,28,37,44,64,25,73,21,23,35,49,23};
int k = g.nextInt(f.length);
select(f, 0, f.length, k);
if (is_partitioned(f, 0, f.length, k))
System.out.printf("Test 1-%d: Passed\n", n);
else
System.out.printf("Test 1-%d: Failed\n", n);
}
int[] a = {8, 2, 7, 5, 1};
if (median(a) == 5.0)
System.out.println("Test 2: Passed");
else
System.out.println("Test 2: Failed");
int[] b = {6, 2, 8, 2, 7, 1};
if (median(b) == 4.0)
System.out.println("Test 3: Passed");
else
System.out.println("Test 3: Failed");
int[] c = {62,88,59,94,4,71,26,17,44,28,37,44,64,25,73,21,23,35,49,23};
if (median(c) == 40.5)
System.out.println("Test 4: Passed");
else
System.out.println("Test 4: Failed");
}
}
Beinagrind fyrir C
#include <stdio.h>
#include <time.h>
#define NELEMS(x) (sizeof(x) / sizeof(x[0]))
// Notkun: select(f,i,j,k)
// Fyrir: f[i..j-1] er svæði í fylkinu f, i <= k < j
// f[i..j-1] má vera óraðað.
// Eftir: Búið er að víxla gildunum í f[i..j-1] þannig
// að f[i..k-1] <= f[k] <= f[k+1..j-1].
void select(int *f, int i, int j, int k)
{
// ...
}
// Notkun: m = median(f);
// Fyrir: Ekkert
// Eftir: m er miðgildi f
double median(int *f, int n)
{
// ...
}
void swap(int *f, int a, int b)
{
int tmp = f[a];
f[a] = f[b];
f[b] = tmp;
}
// Notkun: k = partition(f,i,j,s);
// Fyrir: f[i..j-1] er löglegt svæði í f,
// i <= s < j
// f[s] er pivot gildi til að skipta eftir
// Eftir: Búið er að víxla gildum í svæðinu þ.a.
// f[i..k-1] <= f[k] <= f[k+1..j-1]
// Gildið í sæti k var upphaflega í sæti s.
int partition(int *f, int i, int j, int s)
{
int p = f[s];
int n = i+1;
int t;
swap(f, i, s);
for (t = i+1; t != j; t++)
{
// [p| < p | >= p | ??? ]
// i n t j
if (f[t] < p)
{
swap(f, t, n);
n++;
}
}
// [p| < p | >= p ]
// i n j
n--;
swap(f, i, n);
// [ < p |p| >=p ]
// i n j
return n;
}
// Notkun: b = is_partitioned(f,i,j,k)
// Fyrir: f[i..j-1] er svæði í fylkinu f, i <= k < j
// f[i..j-1] má vera óraðað.
// Eftir: b er satt þþaa. að
// f[i..k-1] <= f[k] <= f[k+1..j-1].
int is_partitioned(int *f, int i, int j, int k)
{
int n;
for (n = i; n != k; n++)
if (f[n] > f[k])
return 0;
for (n = k; n != j; n++)
if (f[n] < f[k])
return 0;
return 1;
}
int main(void)
{
int n;
srand(time(NULL));
for (n = 0; n < 5; n++)
{
int f[] = {62,88,59,94,4,71,26,17,44,28,37,44,64,25,73,21,23,35,49,23};
int k = rand() % NELEMS(f);
select(f, 0, NELEMS(f), k);
if (is_partitioned(f, 0, NELEMS(f), k))
printf("Test 1-%d: Passed\n", n);
else
printf("Test 1-%d: Failed\n", n);
}
int a[] = {8, 2, 7, 5, 1};
if (median(a, NELEMS(a)) == 5.0)
printf("Test 2: Passed\n");
else
printf("Test 2: Failed\n");
int b[] = {6, 2, 8, 2, 7, 1};
if (median(b, NELEMS(b)) == 4.0)
printf("Test 3: Passed\n");
else
printf("Test 3: Failed\n");
int c[] = {62,88,59,94,4,71,26,17,44,28,37,44,64,25,73,21,23,35,49,23};
if (median(c, NELEMS(c)) == 40.5)
printf("Test 4: Passed\n");
else
printf("Test 4: Failed\n");
}
Dæmi 2 (2 stig) - Bilað partition
Í partition fallinu hér fyrir neðan leynist ein villa. Finnið og lagið hana. Skrifið jafnframt fastayrðingu og eftirskilyrði fyrir lykkjuna ásamt tveimur öðrum stöðulýsingum innan í lykkjunni á þar til gerðum stöðum.
Notið ospd-random.txt til að prófa forritið. Forritið ætti að prenta út "SUCCESS".
Prófun
hhg@hhg:~/t2/V8/d2$ java Quicksort < ospd-random.txt SUCCESS hhg@hhg:~/t2/V8/d2$
Java kóði
import java.util.Scanner;
import java.util.ArrayList;
public class Quicksort
{
// Notkun: sort(a, lo, hi);
// Fyrir: a[lo..hi] er löglegt svæði
// Eftir: Búið er að raða a[lo..hi]
private static void sort(String[] a, int lo, int hi)
{
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
// Notkun: k = partition(a, lo, hi);
// Fyrir: a[lo..hi] er löglegt svæði
// Eftir: Búið er að víxla gildunum í f[lo..hi] þannig
// að f[lo..k-1] <= f[k] <= f[k+1..hi].
private static int partition(String[] a, int lo, int hi)
{
int i = lo + 1;
int j = hi;
String v = a[lo];
while (true)
{
// Skrifið fastayrðingu lykkju hér
while (i < hi && less(a[i], v))
i++;
// Skrifið stöðulýsingu fyrir i og a[i] hér
while (j > lo && less(v, a[j]))
j--;
// Skrifið stöðulýsingu fyrir j og a[j] hér
if (i >= j) break;
swap(a, i, j);
i++;
j++;
}
// Hér vantar eftirskilyrði (post-condition)
swap(a, lo, j);
return j;
}
// er v < w ?
private static boolean less(String v, String w)
{
return v.compareTo(w) < 0;
}
// víxlar a[i] og a[j]
private static void swap(Object[] a, int i, int j)
{
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private static boolean isSorted(String[] a, int lo, int hi)
{
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[i-1]))
return false;
return true;
}
public static void main(String[] args)
{
ArrayList<String> q = new ArrayList<String>();
Scanner scan = new Scanner(System.in);
while (scan.hasNext())
{
q.add(scan.nextLine());
}
String[] f = q.toArray(new String[0]);
sort(f, 0, f.length - 1);
if (isSorted(f, 0, f.length - 1))
System.out.println("SUCCESS");
else
System.out.println("FAILED");
}
}
C kóði
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// Notkun: sort(a, lo, hi);
// Fyrir: a[lo..hi] er löglegt svæði
// Eftir: Búið er að raða a[lo..hi]
void sort(char *a[], int lo, int hi)
{
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
void swap(char *a[], int i, int j)
{
char *swap = a[i];
a[i] = a[j];
a[j] = swap;
}
// Notkun: k = partition(a, lo, hi);
// Fyrir: a[lo..hi] er löglegt svæði
// Eftir: Búið er að víxla gildunum í f[lo..hi] þannig
// að f[lo..k-1] <= f[k] <= f[k+1..hi].
int partition(char *a[], int lo, int hi)
{
int i = lo + 1;
int j = hi;
char *v = a[lo];
while (1)
{
// Skrifið fastayrðingu lykkju hér
while (i < hi && strcmp(a[i], v) < 0)
i++;
// Skrifið stöðulýsingu fyrir i og a[i] hér
while (j > lo && strcmp(v, a[j]) < 0)
j--;
// Skrifið stöðulýsingu fyrir j og a[j] hér
if (i >= j) break;
swap(a, i, j);
i++;
j++;
}
// Hér vantar eftirskilyrði (post-condition)
swap(a, lo, j);
return j;
}
int isSorted(char *a[], int lo, int hi)
{
int i;
for (i = lo + 1; i <= hi; i++)
if (strcmp(a[i], a[i-1]) < 0)
return 0;
return 1;
}
char *readline(FILE *fp)
{
size_t size = 0;
size_t len = 0;
size_t last = 0;
char *buf = NULL;
while (!feof(fp))
{
size += BUFSIZ;
buf = realloc(buf, size);
if (fgets(buf+last, size-last, fp) == NULL)
break;
len = strlen(buf);
last = len - 1;
if (buf[last] == '\n')
break;
}
if (len == 0)
{
free(buf);
return NULL;
}
return buf;
}
int main(void)
{
char **lines;
size_t size = 65536;
int n = 0;
lines = malloc(sizeof(char *) * size);
while (1)
{
if (n >= size)
{
size *= 2;
lines = realloc(lines, sizeof(char *) * size);
}
char *line = readline(stdin);
if (line == NULL)
break;
lines[n++] = line;
}
sort(lines, 0, n-1);
if (isSorted(lines, 0, n - 1))
printf("SUCCESS\n");
else
printf("FAILED\n");
}
Dæmi 3 (2 stig) - Forgangsbiðröð byggð á fylki í engri sérstakri röð
Klárið að útfæra beinagrindina samkvæmt þeirri gagnaskipan sem er lýst efst í klasanum.
Skrifið fastayrðingu fyrir sérhverja lykkju sem þið notið. Greinið frá tímaflækju deleteMin og Put.
Beinagrind fyrir C
Beinagrind fyrir C ásamt Makefile
Beinagrind fyrir Java
public class PriQueue
{
// Gildin í forgangsbiðröðinni eru í f[0..n-1]
// í engri sérstakri röð.
private String[] f;
private int n;
private int max;
// Notkun: pq = new PriQueue(max);
// Fyrir: max > 0
// Eftir: pq er ný tóm forgangsbiðröð með pláss fyrir
// max gildi
public PriQueue(int max)
{
// ...
}
// Notkun: s = pq.deleteMin();
// Fyrir: pq er ekki tóm.
// Eftir: s er eitt minnsta stakið sem var
// í pq. s hefur verið fjarlægt úr pq.
public String deleteMin()
{
// ...
}
// Notkun: pq.Put(s);
// Fyrir: pq er ekki full.
// Eftir: s hefur verið bætt við pq.
public void Put(String s)
{
// ...
}
// Notkun: n = pq.Count();
// Eftir: n er fjöldi staka í pq.
public int Count()
{
// ...
}
// Notkun: b = pq.isFull();
// Eftir: b er satt þþaa. pq sé full.
public boolean isFull()
{
// ...
}
public static void main(String[] args)
{
PriQueue pq = new PriQueue(100);
pq.Put("F");
pq.Put("B");
pq.Put("D");
pq.Put("C");
pq.Put("A");
pq.Put("H");
while (pq.Count() > 0)
System.out.println(pq.deleteMin());
}
}
Dæmi 4 (2 stig) - Forgangsbiðröð byggð á fylki í minnkandi röð
Klárið að útfæra beinagrindina samkvæmt þeirri gagnaskipan sem er lýst efst í klasanum. Útfærið Put aðferðina með samskonar innsetningu og við notuðum í insertion sort.
Skrifið fastayrðingu fyrir sérhverja lykkju sem þið notið. Greinið frá tímaflækju deleteMin og Put.
Beinagrind fyrir C
Beinagrind fyrir C ásamt Makefile
Beinagrind fyrir Java
public class PriQueue
{
// Gildin í forgangsbiðröðinni eru í f[0..n-1]
// í minnkandi röð frá f[0] til f[n-1], þ.e.
// f[0] er stærsta gildið og f[n-1] er minnsta gildið.
private String[] f;
private int n;
private int max;
// Notkun: pq = new PriQueue(max);
// Fyrir: max > 0
// Eftir: pq er ný tóm forgangsbiðröð með pláss fyrir
// max gildi
public PriQueue(int max)
{
// ...
}
// Notkun: s = pq.deleteMin();
// Fyrir: pq er ekki tóm.
// Eftir: s er eitt minnsta stakið sem var
// í pq. s hefur verið fjarlægt úr pq.
public String deleteMin()
{
// ...
}
// Notkun: pq.Put(s);
// Fyrir: pq er ekki full.
// Eftir: s hefur verið bætt við pq.
public void Put(String s)
{
// ...
}
// Notkun: n = pq.Count();
// Eftir: n er fjöldi staka í pq.
public int Count()
{
// ...
}
// Notkun: b = pq.isFull();
// Eftir: b er satt þþaa. pq sé full.
public boolean isFull()
{
// ...
}
public static void main(String[] args)
{
PriQueue pq = new PriQueue(100);
pq.Put("F");
pq.Put("B");
pq.Put("D");
pq.Put("C");
pq.Put("A");
pq.Put("H");
while (pq.Count() > 0)
System.out.println(pq.deleteMin());
}
}
Dæmi 5 (2 stig) - Tvítré í fylki
Gefum okkur eftirfarandi tré þar sem hver hnútur í trénu hefur að hámarki tvö börn:
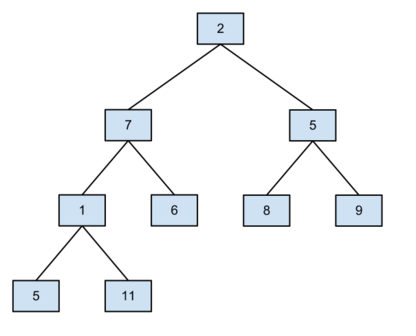
Við skulum geyma tréið í fylki með eftirfarandi sætaskipan:
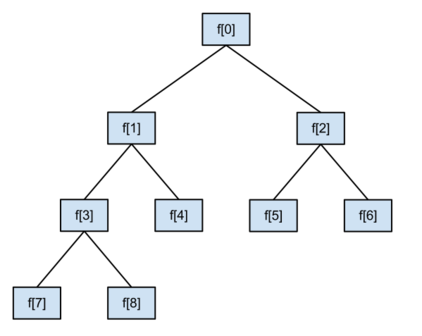
Almennt þá gilda eftirfarandi reglur um slíka sætaskipan:
- Hnútur f[i] hefur vinstra barn f[2*i + 1] (ef það er innan fylkisins)
- Hnútur f[i] hefur hægra barn f[2*i + 2] (ef það er innan fylkisins)
- Hnútur f[i] hefur foreldri f[(i-1)/2] (ef það er innan fylkisins)
Í beinagrindinni hér fyrir neðan eru gefin ýmis föll sem vinna með tréð. Þar eru m.a. föll sem ferðast um tréð og prenta út gildi í in-order, pre-order eða post-order röð. Þið getið lesið ykkur til um slíkar raðanir á Wikipedia eða Google. Þið eigið að skrifa tvö auka föll:
- printLeaves: prentar út öll lauf í trénu í pre-order röð
- printRootPath: prentar út öll gildi í trénu á veginum frá tilteknum hnút upp að rótinni
Beinagrind fyrir Java
public class BinaryTreeArray
{
public static void printInOrder(int[] f, int n)
{
if (n >= f.length)
return;
printInOrder(f, 2*n+1);
System.out.printf("%d ", f[n]);
printInOrder(f, 2*n+2);
}
public static void printPreOrder(int[] f, int n)
{
if (n >= f.length)
return;
System.out.printf("%d ", f[n]);
printPreOrder(f, 2*n+1);
printPreOrder(f, 2*n+2);
}
public static void printPostOrder(int[] f, int n)
{
if (n >= f.length)
return;
printPostOrder(f, 2*n+1);
printPostOrder(f, 2*n+2);
System.out.printf("%d ", f[n]);
}
// Notkun: printLeaves(f, n);
// Eftir: Búið er að prenta öll lauf
// í trénu sem hefur rótina f[n]
public static void printLeaves(int[] f, int n)
{
// ...
}
// Notkun: printRootPath(f, n);
// Fyrir: f inniheldur tvítré
// 0 <= n < f.length
// Eftir: Búið er að prenta út öll gildin í trénu
// f á veginum frá f[n] upp að rótinni f[0]
public static void printRootPath(int[] f, int n)
{
// ...
}
public static void printSubtree(int level, int[] f, int n)
{
if (level > 0)
System.out.print(" ");
int leaves = f.length/2;
if (n < leaves)
{
System.out.print("(" + f[n]);
printSubtree(level+1, f, 2*n+1);
printSubtree(level+1, f, 2*n+2);
System.out.print(")");
} else if (n < f.length)
{
System.out.printf("%d", f[n]);
} else
{
System.out.print("()");
}
}
public static void main(String[] args)
{
/*
* tree in f:
* 2
* / \
* / \
* / \
* 7 5
* / \ / \
* 1 6 8 9
* / \
* 5 11
*
* rules:
* f[i] has left child f[2*i + 1]
* f[i] has right child f[2*i + 2]
* f[i] has parent f[(n-1)/2]
*/
int[] f = {2,7,5,1,6,8,9,5,11};
System.out.println("Items:");
for (int i = 0; i < f.length; i++)
System.out.printf("f[%d] = %d\n", i, f[i]);
System.out.println();
System.out.println("List representation of tree:");
printSubtree(0, f, 0);
System.out.println();
System.out.println();
System.out.println("In-order traversal:");
printInOrder(f, 0);
System.out.println();
System.out.println();
System.out.println("Pre-order traversal:");
printPreOrder(f, 0);
System.out.println();
System.out.println();
System.out.println("Post-order traversal:");
printPostOrder(f, 0);
System.out.println();
System.out.println();
System.out.println("Pre-order traversal of the leaf nodes:");
printLeaves(f, 0);
System.out.println();
System.out.println("Expecting:");
System.out.println("5 11 6 8 9");
System.out.println();
System.out.println("Path to root from leaf f[8] == 11");
printRootPath(f, 8);
System.out.println("Expecting:");
System.out.println("11 1 7 2");
System.out.println();
System.out.println("Path to root from leaf f[4] == 6");
printRootPath(f, 4);
System.out.println("Expecting:");
System.out.println("6 7 2");
System.out.println();
System.out.println("Path to root from leaf f[5] == 8");
printRootPath(f, 5);
System.out.println("Expecting:");
System.out.println("8 5 2");
}
}
Beinagrind fyrir C
#include <stdio.h>
#define NELEMS(x) (sizeof(x) / sizeof(x[0]))
static void printInOrder(int *f, int size, int n)
{
if (n >= size)
return;
printInOrder(f, size, 2*n+1);
printf("%d ", f[n]);
printInOrder(f, size, 2*n+2);
}
static void printPreOrder(int *f, int size, int n)
{
if (n >= size)
return;
printf("%d ", f[n]);
printPreOrder(f, size, 2*n+1);
printPreOrder(f, size, 2*n+2);
}
static void printPostOrder(int *f, int size, int n)
{
if (n >= size)
return;
printPostOrder(f, size, 2*n+1);
printPostOrder(f, size, 2*n+2);
printf("%d ", f[n]);
}
static void printLeaves(int *f, int size, int n)
{
// ...
}
static void printRootPath(int *f, int size, int n)
{
// ...
}
static void printSubtree(int level, int *f, int size, int n)
{
if (level > 0)
printf(" ");
int leaves = size/2;
if (n < leaves)
{
printf("(%d", f[n]);
printSubtree(level+1, f, size, 2*n+1);
printSubtree(level+1, f, size, 2*n+2);
printf(")");
} else if (n < size)
{
printf("%d", f[n]);
} else
{
printf("()");
}
}
int main(void)
{
/*
* tree in f:
* 2
* / \
* / \
* / \
* 7 5
* / \ / \
* 1 6 8 9
* / \
* 5 11
*
* rules:
* f[i] has left child f[2*i + 1]
* f[i] has right child f[2*i + 1]
* f[i] has parent f[(n-1)/2]
*/
int f[] = {2,7,5,1,6,8,9,5,11};
int i;
printf("Items:\n");
for (i = 0; i < NELEMS(f); i++)
printf("f[%d] = %d\n", i, f[i]);
printf("\n");
printf("List representation of tree:\n");
printSubtree(0, f, NELEMS(f), 0);
printf("\n");
printf("\n");
printf("In-order traversal:\n");
printInOrder(f, NELEMS(f), 0);
printf("\n");
printf("\n");
printf("Pre-order traversal:\n");
printPreOrder(f, NELEMS(f), 0);
printf("\n");
printf("\n");
printf("Post-order traversal:\n");
printPostOrder(f, NELEMS(f), 0);
printf("\n");
printf("\n");
printf("Pre-order traversal of the leaf nodes:\n");
printLeaves(f, NELEMS(f), 0);
printf("\n");
printf("Expecting:\n");
printf("5 11 6 8 9\n");
printf("\n");
printf("Path to root from leaf f[8] == 11\n");
printRootPath(f, NELEMS(f), 8);
printf("Expecting:\n");
printf("11 1 7 2\n");
printf("\n");
printf("Path to root from leaf f[4] == 6\n");
printRootPath(f, NELEMS(f), 4);
printf("Expecting:\n");
printf("6 7 2\n");
printf("\n");
printf("Path to root from leaf f[5] == 8\n");
printRootPath(f, NELEMS(f), 5);
printf("Expecting:\n");
printf("8 5 2\n");
}